Медіана (статистика)
Медіа́на (англ. median) — в статистиці це величина ознаки, що розташована по середині ранжованого ряду вибірки[1], тобто — це величина, що розташована в середині ряду величин, розташованих у зростаючому або спадному порядку[2]; в теорії ймовірності — характеристика розподілення випадкової величини.
Медіана ділить ряд значень ознаки на дві рівні частини, по обидві частини від неї розміщується однакова кількість одиниць сукупності.[1]
Медіана є квантилем порядку 1/2. Позначається як x~displaystyle tilde x або x1/2displaystyle x_1/2,.
Зміст
1 Визначення
2 Скінченна множина чисел
3 Історія
4 Медіана варіаційного ряду
5 Розподіл імовірностей
5.1 Медіани окремих розподілів
6 Сукупності
6.1 Властивість оптимальності
6.2 Одномодальні розподіли
6.3 Нерівність, що пов'язує середнє значення і медіану
7 Медіана як об'єктивний оцінювач
8 Примітки
9 Див. також
10 Посилання
Визначення |
Медіаною функції розподілу Fdisplaystyle F називається таке число x~displaystyle tilde x, що:[3]
F(x~)=1/2displaystyle F(tilde x)=1/2,
або:[4]
P(X<x~)=P(X>x~)=1/2displaystyle P(X<tilde x)=P(X>tilde x)=1/2,
тобто, ймовірність того, що випадкова величина матиме значення більше або менше за медіану однакова і дорівнює 1/2.
Якщо функція розподілу строго монотонна, то медіана визначається однозначно, в протилежному випадку, розв'язком рівняння x~=F−1(x)displaystyle tilde x=F^-1(x) є відрізок [x_,x¯]displaystyle [underline x,overline x]. З точки зору теорії ймовірностей, значення з цього відрізку можна не розглядати. Таким чином, неоднозначність цього рівняння неістотна. Аби уникнути пов'язаних з цієї неоднозначностей проблем, медіаною можна вважати найменший корінь рівняння: x~=x_displaystyle tilde x=underline x.[3]
![displaystyle [underline x,overline x]](https://wikimedia.org/api/rest_v1/media/math/render/svg/238b6b9fb67eae4238d1eabf6331dfc134bd2320)
З геометричної точки зору, вертикальна пряма x=x~displaystyle x=tilde x, що проходить через точку з абсцисою x~displaystyle tilde x ділить площу фігури під кривою функції розподілу на дві рівні частини.[4]
Скінченна множина чисел |
Медіану скінченної множини чисел можна знайти впорядкувавши їх в порядку зростання, від найменшого числа до найбільшого.
Якщо кількість чисел непарна, обирається те що знаходиться по середині. Наприклад, нехай існує такий набір чисел
- 1, 3, 3, 6, 7, 8, 9
Цей список містить сім чисел. Медіаною є четверте із них, що є числом 6.
Якщо кількість спостережень парна, тоді не існує єдиного значення по середині; тоді медіану зазвичай визначають як середнє значення між двома числами по середині.[5][6] Наприклад, для наступного набору
- 1, 2, 3, 4, 5, 6, 8, 9
медіана є середнім значенням для двох чисел по середині: вона дорівнюватиме (4 + 5)/2, тобто 4.5 або 412displaystyle 4frac 12.
Для знаходження позиції середнього числа в вибірці із n послідовно впорядкованих чисел використовується формула (n + 1) ÷ 2. Ця формула повертає або позицію середнього числа (для непарної кількості значень) або знаходиться по середині між двома точками. Наприклад, при кількості в 14 значень, формула поверне 7.5, тоді медіану необхідно розраховувати як середнє значення між сьомим і восьмим значенням. Таким чином медіану можна представити наступною формулою:
- median(a)=a⌊#x÷2⌋+a⌊#x÷2+0.5⌋2displaystyle mathrm median (a)=frac a_lfloor #xdiv 2rfloor +a_lfloor #xdiv 2+0.5rfloor 2
| Тип | Опис | Приклад | Результат |
|---|---|---|---|
Середнє арифметичне | Сума всіх значень вибірки поділена на кількість цих елементів вибірки: x¯=1n∑i=1nxidisplaystyle scriptstyle bar x=frac 1nsum _i=1^nx_i | (1+2+2+3+4+7+9) / 7 | 4 |
| Медіана | Середнє значення, що відокремлює більшу половину і меншу половину вибірки | 1, 2, 2, 3, 4, 7, 9 | 3 |
Мода | Значення, що зустрічається у вибірці найчастіше | 1, 2, 2, 3, 4, 7, 9 | 2 |
Найчастіше медіану застосовують для скошених (не симетричних) розподілів, де вона дозволяє підсумувати різницю від арифметичного середнього. Розглянемо мультимножину 1, 2, 2, 2, 3, 14 . В даному випадку медіана дорівнює 2, (так само як і мода), і її можна розглядати як більш придатний індикатор центральної тенденції (що менш чутливий до зміщення при наявності виключно великого значення серед даних) ніж арифметичне середнє, що дорівнює 4.
Медіана — дуже популярна міра підсумкової статистики, оскільки її просто зрозуміти і легко розрахувати, а також вона більш стійка до можливих наявних викидів у вибірці, в порівнянні із середнім значенням. Часто зустрічається твердження про емпіричний зв'язок між відносним знаходженням середнього значення і медіани для скошених розподілів, що насправді не є вірним в загальному випадку.[7] Однак, існує багато залежностей між абсолютною різницею між ними.
Історія |
Поняття медіани походить з книги Едварда Райта про навігацію («Помилки в навігації» 1599 року), в розділі з приводу визначення розташування за допомогою компаса. Він зрозумів, що вірогідніше всього, це значення може бути правильним в серіях спостережень.
У 1757 році Роджер Джосеф Бошкович розвивав регресивний метод, заснований на нормі L1 і на медіані[8]. У 1774 році Лаплас запропонував використати медіану як стандартний оцінювач значення пізнішого pdf. Специфічні критерії мали мінімізувати очікувану величину помилки; |α−α∗|displaystyle , де α* — оцінка, і α — справжня цінність.
Критерій Лапласа був загалом знехтуваний протягом 150 років на користь найменшого методу квадратів Гауса і Легенгре, який мінімізує значення (α−α∗)2displaystyle (alpha -alpha ^*)^2, щоб отримати середину[9]. Поширення як типового означення, так і типової медіани були визначені Лапласом на початку 1800 року[10]. Антуан Августин Курно в 1843 році був першим, хто використав термін «медіана», як значення, яке ділить розподіл вірогідності на дві рівні частини.
Густав Теодор Фішнер використовував медіану (Centralwerth) в соціологічних і психологічних явищах[11].
Густав Фішнер популяризував медіану у формальному аналізі даних, хоча це вперше зробив Лаплас[11]. Франциск Гальтон вжив англійський термін «медіана» в 1881 році,[12] раніше використовуючи «середина найбільшого значення» (1869 рік) і як «середина» в 1880 році.
Медіана варіаційного ряду |
Медіаною називають варіанту, що ділить варіаційний ряд на дві частини з рівною кількістю варіант. Якщо кількість варіант непарна (n=2k+1displaystyle n=2k+1), то x~=xk+1displaystyle tilde x=x_k+1, у випадку парної кількості варіант (n=2kdisplaystyle n=2k), медіана дорівнює:[13]
x~=(xk+xk+1)2displaystyle tilde x=frac (x_k+x_k+1)2.
Наприклад, для ряду 2 3 5 6 7 медіана дорівнює 5; для ряду 2 3 5 6 7 9 медіана дорівнює (5 + 6)/2 = 5.5.
Розподіл імовірностей |
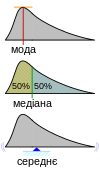
Геометрична візуалізація моди, медіани і середнього значення довільної функції густини імовірностей.[14]
Для будь-якого розподілу імовірностей в множині дійсних чисел R із кумулятивною функцією розподілу F, не залежно від того чи є це будь-яким з неперервних розподілів імовірності, зокрема абсолютно неперервний розподіл (що має функцію густини імовірності), або дискретний розподіл імовірностей, медіаною за визначенням є будь-яке дійсне число m яке задовольняє наступним нерівностям:
- P(X≤m)≥12 і P(X≥m)≥12displaystyle operatorname P (Xleq m)geq frac 12text і operatorname P (Xgeq m)geq frac 12,!
або, еквівалентні нерівності
- ∫(−∞,m]dF(x)≥12 і ∫[m,∞)dF(x)≥12displaystyle int _(-infty ,m]dF(x)geq frac 12text і int _[m,infty )dF(x)geq frac 12,!
![displaystyle int _(-infty ,m]dF(x)geq frac 12text і int _[m,infty )dF(x)geq frac 12,!](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc133cdeddb48f47a14215c3d68dcd1ef4a55a49)
в яких використовується інтеграл Лебега-Стілтьєса[en]. Для будь-якого абсолютно неперервного розподілу імовірностей із функцією густини імовірностей ƒ, медіана задовольняє умовам:
- P(X≤m)=P(X≥m)=∫−∞mf(x)dx=12.displaystyle operatorname P (Xleq m)=operatorname P (Xgeq m)=int _-infty ^mf(x),dx=frac 12.,!
Будь-який розподіл імовірностей в множині R має принаймні одну медіану, але в окремих випадках може існувати більше ніж одна медіана. Зокрема, якщо розподіл імовірностей дорівнює нулю в інтервалі [a, b], а кумулятивна функція розподілу в точці a приймає значення 1/2, будь-яке значення між a і b також буде медіаною.
Медіани окремих розподілів |
Медіани певних типів розподілів можна легко розрахувати за допомогою їх параметрів; крім того, цей розрахунок існує навіть для деяких розподілів, яким бракує можливості добре визначити середнє, наприклад для розподілу Коші:
- Медіана симетричного унімодального розподілу[en] збігається із модою.
- Медіана симетричного розподілу[en], який має середнє значення μ також приймає значення μ.
- Медіана нормального розподілу із середнім μ і дисперсією σ2 дорівнює μ. Насправді для нормального розподілу дійсним є те, що середнє = медіані = моді.
- Медіана рівномірного розподілу у інтервалі [a, b] дорівнює (a + b) / 2, що також є середнім значенням.
- Медіана розподілу Коші із параметром локації x0 і параметром масштабу y дорівнює x0, параметру локації.
- Медіана експоненційного розподілу із коефіцієнтом норми λ дорівнює натуральному логарифму по 2 розділеному на коефіцієнт норми: λ−1ln 2.
- Медіана розподілу Вейбула із параметром форми k і параметром масштабу λ дорівнює λ(ln 2)1/k.
Сукупності |
Властивість оптимальності |
Середня абсолютна похибка дійсної змінної c відносно випадкової величини X визначається як:
- E(|X−c|)X-cright
За умови, що розподіл імовірностей величини X є таким, що вищенаведене сподівання існує, тоді m є медіаною величини X тоді і тільки тоді, коли m мінімізує середню абсолютну похибку відносно X.[15] Зокрема, m є вибірковою медіаною, тоді і лише тоді, коли m мінімізує арифметичне середнє абсолютних відхилень.
У більш загальному випадку, медіана визначається як мінімум наступного виразу
- E(|X−c|−|X|),X
Це визначення медіани на основі оптимізації є корисним у статистичному аналізі даних, наприклад, у кластеризації k-медіан[en].
Одномодальні розподіли |
Порівняння середнього, медіані і моди двох Логнормальних розподілів із різним коефіцієнтом асиметрії.
Для випадку із одномодальним розподілом можна показати що медіана X~displaystyle tilde X і середнє X¯displaystyle bar X знаходяться не далі ніж на величину (3/5)1/2 ≈ 0.7746 стандартних відхилень одне від одного.[16] У символьній формі це виглядає так:
- |X~−X¯|σ≤(35)12displaystyle frac tilde X-bar Xrightsigma leq left(frac 35right)^frac 12
де |·| це абсолютне значення.
Аналогічне відношення існує для медіани і моди: вони знаходяться в межах 31/2 ≈ 1.732 стандартних відхилень одна від одної:
- |X~−mode|σ≤312.displaystyle frac sigma leq 3^frac 12.
Нерівність, що пов'язує середнє значення і медіану |
Якщо розподіл має скінченну дисперсію, тоді відстань між медіаною і середнім обмежена величиною одного стандартного відхилення.
Ця межа була доведена,[17] за допомогою подвійного використання нерівності Єнсена, як наведено далі. Маємо
- |μ−m|=|E(X−m)|≤E(|X−m|)≤E(|X−μ|)≤E((X−μ)2)=σ.displaystyle =
Перша і третя нерівність були отримані з нерівності Єнсена, що застосована до функції із абсолютним значенням і квадратичної функції, кожна з яких є опуклою. Друга нерівність отримана з факту, що медіана мінімізує функцію абсолютного відхилення[en]
- a↦E(|X−a|).displaystyle amapsto operatorname E (
Також доведення можна отримати із нерівності Кантеллі[en].[18]
Цей результат можна узагальнити аби отримати мультиваріативний варіант нерівності,[19] наступним чином:
- ‖μ−m‖=‖E(X−m)‖≤E‖X−m‖≤E(‖X−μ‖)≤E(‖X−μ‖2)=trace(var(X))displaystyle mu -m
де m є просторовою медіаною, яка мінімізує функцію
a↦E(‖X−a‖).displaystyle amapsto operatorname E ( Просторова медіана є унікальною коли два або більшу кількість вимірів вибірки.[20][21] В аналогічному доведенні використовують односторонню нерівність Чебишова; вона з'являється у нерівності параметрів розташування і масштабу розподілу.
Медіана як об'єктивний оцінювач |
Гаус зауважив, що будь-який об'єктивний оцінювач мінімізує ризик (очікувану втрату) відносно функції помилкової втрати. На думку Лапласа, медіана, як об'єктивний оцінювач мінімізує ризик відносно функції втрати абсолютного відхилення.
Інші функції втрати застосовують в статистичній теорії, особливо при перевірці статистичної надійності. Теорію об'єктивного оцінювача, започаткував Джордж Браун в 1947 році[22].
Оцінка одного розмірного параметра θ, буде об'єктивним оцінювачем для медіани, якщо, для сталої θ, медіана поширення оцінки знаходиться в значенні θ , тобто, відхилення трапляються не так часто.
Подальші властивості медіани, як об'єктивного оцінювача були досліджені[23][24][25][26]. Зокрема, медіана, як об'єктивний оцінювач існує у випадках, де не можливо максимуму вірогідності. Медіани, як об'єктивні оцінювачі інваріантні під один-до-одного, перетвореннями.
Примітки |
↑ аб Социологический энциклопедический словарь / Ред.-координатор Г. В. Осипов.-М., 1998
↑ Медіана — Розум.org.ua
↑ аб Козлов М. В., Прохоров А. В. (1987). Введение в математическую статистику. Изд-во МГУ.
↑ аб Кремер Н. Ш. (2004). Теория вероятностей и математическая статистика. Юнити. ISBN 5-238-00573-3.
↑ Weisstein, Eric W. Statistical Median(англ.) на сайті Wolfram MathWorld.
↑ Simon, Laura J.; "Descriptive statistics" Архівовано 2010-07-30 у en:Wayback Machine., Statistical Education Resource Kit, Pennsylvania State Department of Statistics
↑ Journal of Statistics Education, v13n2: Paul T. von Hippel. amstat.org.
↑ Stigler, S. M. (1986). The History of Statistics: The Measurement of Uncertainty Before 1900. Harvard University Press. ISBN 0674403401.
↑ Jaynes, E.T. (2007). Probability theory: the logic of science (5. print. ed.). Cambridge [u.a.]: Cambridge Univ. Press. p. 172. ISBN 978-0-521-59271-0.
↑ Laplace PS de (1818) Deuxième supplément à la Théorie Analytique des Probabilités, Paris, Courcier.
↑ аб Keynes, J.M. (1921) A Treatise on Probability. Pt II Ch XVII § 5 (p 201) (2006 reprint, Cosimo Classics, ISBN 9781596055308 : multiple other reprints).
↑ Galton F (1881) «Report of the Anthropometric Committee» pp 245–260. Report of the 51st Meeting of the British Association for the Advancement of Science.
↑ Гмурман В. Е. (2003). Теория вероятностей и математическая статистика (вид. 9-те). Высшая школа.
↑ AP Statistics Review - Density Curves and the Normal Distributions. Процитовано 16 March 2015.
↑ Stroock, Daniel (2011). Probability Theory. Cambridge University Press. с. 43. ISBN 978-0-521-13250-3.
↑ An Error Occurred Setting Your User Cookie. siam.org.
↑ Mallows, Colin (August 1991). Another comment on O'Cinneide. The American Statistician 45 (3): 257. doi:10.1080/00031305.1991.10475815.
↑ K.Van Steen Notes on probability and statistics
↑ Piché, Robert (2012). Random Vectors and Random Sequences. Lambert Academic Publishing. ISBN 978-3659211966.
↑ Kemperman, Johannes H. B. (1987). The median of a finite measure on a Banach space: Statistical data analysis based on the L1-norm and related methods. У Dodge, Yadolah. Papers from the First International Conference held at Neuchâtel, August 31–September 4, 1987 (Amsterdam: North-Holland Publishing Co.): 217–230. MR 949228.
↑ Milasevic, Philip; Ducharme, Gilles R. (1987). Uniqueness of the spatial median. Annals of Statistics 15 (3): 1332–1333. MR 902264. doi:10.1214/aos/1176350511.
↑ Brown, George W. (1947). «On Small-Sample Estimation». Annals of Mathematical Statistics 18 (4): 582–585. doi:10.1214/aoms/1177730349. JSTOR 2236236.
↑ Lehmann, Erich L. (1951). «A General Concept of Unbiasedness». Annals of Mathematical Statistics 22 (4): 587–592. doi:10.1214/aoms/1177729549.JSTOR 2236928.
↑ Birnbaum, Allan (1961). «A Unified Theory of Estimation, I». Annals of Mathematical Statistics 32 (1): 112–135. doi:10.1214/aoms/1177705145. JSTOR 2237612.
↑ van der Vaart, H. Robert (1961). «Some Extensions of the Idea of Bias». Annals of Mathematical Statistics 32 (2): 436–447. doi:10.1214/aoms/1177705051.JSTOR 2237754. MR 125674.
↑ Pfanzagl, Johann; with the assistance of R. Hamböker (1994). Parametric Statistical Theory. Walter de Gruyter. ISBN 3-11-013863-8. MR 1291393.
Див. також |
- Квантиль
Посилання |
Statistical Median. на MathWorld(англ.)
 | Це незавершена стаття з математики. Ви можете допомогти проекту, виправивши або дописавши її. |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Категорія
Портал
Вікісховище
