Ufdjrw

На малюнку зображено провідник, навколо якого існує магнітне поле

Магнітні силові лінії, утворені залізною стружкою на папері, до якого піднесений магніт

Магні́тне по́ле — складова електромагнітного поля, за допомогою якої здійснюється взаємодія між рухомими електрично зарядженими частинками.

Загальний опис

Магнітне поле — складова електромагнітного поля, яка створюється змінним у часі електричним полем, рухомими електричними зарядами або спінами заряджених частинок. Магнітне поле спричиняє силову дію на рухомі електричні заряди. Нерухомі електричні заряди з магнітним полем не взаємодіють, але елементарні частинки з ненульовим спіном, які мають власний магнітний момент, є джерелом магнітного поля і магнітне поле спричиняє на них силову дію, навіть якщо вони перебувають у стані спокою.

Магнітне поле утворюється, наприклад, у просторі довкола провідника, по якому тече струм або довкола постійного магніту.

Магнітне поле є векторним полем, тобто з кожною точкою простору пов'язаний вектор магнітної індукції B displaystyle mathbf B який характеризує величину і напрям магнітого поля у цій точці і може мінятися з плином часу. Поряд з вектором магнітної індукції B displaystyle mathbf B , магнітне поле також описується вектором напруженості H displaystyle mathbf H .

У вакуумі ці вектори пропорційні між собою:

B=kHdisplaystyle mathbf B =kmathbf H ,

де k — константа, що залежить від вибору системи одиниць.

В системі СІ, k=μ0displaystyle k=mu _0 — так званій магнітній проникності вакууму. Деякі системи одиниць, наприклад СГСГ, побудовані так, щоб вектори індукції та напруженості магнітного поля тотожно дорівнювали один одному: k=1 displaystyle k=1 .

Однак у середовищі ці вектори є різними: вектор напруженості H displaystyle mathbf H описує лише магнітне поле створене рухомими зарядами (струмами) ігноруючи поле створене середовищем, тоді як вектор індукції B displaystyle mathbf B враховує ще й вплив середовища:

B=H+4πM,displaystyle mathbf B =mathbf H +4pi mathbf M ,^[1]

де Mdisplaystyle mathbf M  — вектор намагніченості середовища.

Історія

Магніти були відомі з давніх часів, наприклад, їх згадував ще Фалес^[2], проте вперше дослідження магнітного поля були проведені в 1269 році французьким вченим Петром Перегріном (справжнє ім'я П'єр Пелерен де Марикур). Він зробив першу мапу магнітного поля, під час чого відкрив, що силові лінії сходяться до двох точок на магніті, які він назвав полюсами, і дав їм сучасні назви — північний і південний^[3]. Також він відмітив принцип, згідно якому, при розламуванні магніту на дві частини, його полюси не відокремлюються, а утворюються нові. Свої спостереження він описав в праці «Послання про магніт» (Epistola de magnete).

Близько трьох століть потому, Вільям Гільберт повторив досліди Перегріна, а також показав, що Земля також є великим магнітом. Для цього він створив «терелу» — сферичну магнітну модель Землі, а потім, зробивши карту магнітного поля біля неї, зіставив результати з отриманими у 1576 році англійським виробником компасів Робертом Норманом даними щодо магнітного нахилу,.^[4] і довів, що ці дві картини ідентичні. Таким чином була спростована існуюча в ті часи гіпотеза про існування велетенських магнітних гір на полюсах Землі, що притягують стрілку компасу.^[5] Книга Гільберта «Про магніт, магнітні тіла та про великий магніт — Землю» фактично започаткувала наукове вивчення магнетизму.

У 1750 році, Джон Мічел припустив, що сила притягання і відштовхування, що її створює магнітне поле зменшується за квадратичним законом.^[6] У 1750 Шарль Кулон експериментально довів цю гіпотезу, а також неможливість відокремлення полюсів магніту один від одного.^[6] Базуючись на цих результатах, Сімеон-Дені Пуассон вперше побудував успішну модель магнетизму, у якій магнітне поле продукувалося великою кількістю пар північних і південних магнітних полюсів всередині магніту.^[6]

На початку 19 століття три важливих відкриття змінили погляд на магнетизм: у 1819 році Ганс Крістіан Ерстед відкрив, що електричний струм генерує навколо себе магнітне поле, у 1820 Андре-Марі Ампер показав, що паралельні провідники притягуються або відштовхуються, коли по них йде струм (Закон Ампера), і, нарешті, також у 1820 році Жан-Батіст Біо і Фелікс Савар відкрили закон, названий їх іменем (пізніше узагальнений Лапласом), що дозволяв знайти напруженість магнітного поля в будь-якій точці навколо провідника зі струмом.

На основі цих експериментів, Ампер опублікував власну теорію магнетизму у 1825 році. У ній він продемонстрував еквівалентність електричних контурів і магнітів, і припустив, що магнетизм спричинений великою кількістю замкнених потоків зі струмом у магніті, замість магнітних диполів, що фігурували в теорії Пуассона.^[6] Додатковою перевагою цієї теорії було те, що вона пояснювала, чому полюси магніту не можуть бути ізольованими.

У 1831 році Майкл Фарадей відкрив явище електромагнітної індукції, тобто факт, що зміна магнітного поля призводить до виникнення електричного поля. Цей закон зараз відомий як закон електромагнітної індукції Фарадея. Пізніше, Франц Ернст Нейман довів, що для провідника, що рухається в магнітному полі, індукція витікає з закону Ампера.^[6] Під час цього він ввів поняття векторного потенціалу магнітного поля.

У 1850-му, лорд Кельвін, відомий тоді як Вільям Томпсон, почав розрізняти два типи магнітного поля, відомі зараз як H і B. Ці поняття він спочатку застосував до моделі Пуассона, а потім і до моделі Ампера. Також, він показав взаємозв'язок між цими типами.^[6]

Між 1861 і 1865 роками, Джеймс Клерк Максвелл вивів і опублікував рівняння Максвела, що пояснювали і пов'язували усі параметри класичних електричного і магнітного полів. Перші варіанти цих рівнянь були опубліковані у журналі Philosophical Magazine and Journal of Science, під заголовком «Фізичні лінії сили». УТі рівняння були вірними, але неповними. Максвел доповнив їх у своїй статті 1865 року «Динамічна теорія електромагнітного поля» і показав, що світло є електромагнітною хвилею. Генріх Герц експериментально довів це в 1887 році.^[6]

У двадцятому столітті, у зв'язку з появою квантової теорії та теорії відносності, електродинаміка включила їх в себе. Альберт Ейнштейн у своїй роботі 1905 року показав, що розділення електромагнітного поля на електричне і магнітне природнім чином витікає з теорії відносності, і при цьому, не є абсолютним, а залежить від системи відліку.^[7] Пізніше, електродинаміка була переформульована у термінах квантової механіки, утворивши таким чином квантову електродинаміку(КЕД).

Утворення магнітного поля

Постійні магніти

На відміну від електричних зарядів, магнітних зарядів, що створювали б магнітне поле аналогічним чином, не спостерігається. Теоретично такі заряди, які отримали назву магнітних монополів, могли б існувати. В такому випадку електричне і магнітне поле були б повністю симетричними.

Таким чином, найменшою одиницею, яка може створювати магнітне поле, є магнітний диполь. Магнітний диполь відрізняється тим, що в нього завжди є два полюси, в яких починаються і кінчаються силові лінії поля. Мікроскопічні магнітні диполі зв'язані зі спінами елементарних частинок. Частинки з ненульовим спіном — такі як протони, нейтрони і електрони, є елементарними магнітами. Величину магнетизму диполю можна виразити за допомогою магнітного дипольного моменту, що зазвичай називається просто магнітним моментом і позначається літерою m. Магнітний момент макроскопічного шматка речовини може бути обрахований як векторна сума магнітних моментів його атомів. Зазвичай, моменти окремих атомів напрямлені хаотично, і тому компенсують один одного, а загальний магнітний момент речовини є нульовим. Проте, деякі речовини, в першу чергу феромагнетики, тяжіють до впорядкованих станів, при яких магнітні моменти усіх атомів в речовині починають бути напрямленими в одну сторону. Існують дві моделі, що описують магнітне поле елементарних магнітних диполів — модель Гілберта і модель Ампера. Для описів полів у цих моделях використовуються дві різні величини, H і B. За межами магніту вони є однаковими, з точністю до постійного множника, проте всередині магніту їх значення перестають збігатися.

Полюсна модель Гілберта і H-поле

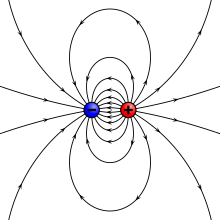
Магнітне поле H, створене двома магнітними зарядами

У цій моделі диполь розглядається як два магнітних заряди, а поле, що вони створюють є аналогічним до поля електричного диполю — його лінії починаються в північному заряді, і закінчуються в південному, не виходячи на нескінченність, так само як лінії електричного поля починаються в позитивному заряді і закінчуються в негативному. Також за аналогією розраховується і магнітний момент такого диполю, що дорівнює m=q_md, де q_m — магнітні заряди а d — відстань між ними.

Модель Гілберта передбачає правильні значення напруженості магнітного поля як всередині так і ззовні магніту, в тому числі той факт, що його напрямок є протилежним до напрямку вектора намагніченості. Проте, полюсна модель має обмеження, пов'язані з тим, що вона спирається на неіснуюче в реальності поняття щільності магнітних зарядів. Через це вона не може пояснити той факт, що полюси магніту неможливо відділити один від одного, а також магнітні властивості рухомих електричних зарядів.

Токова модель Ампера і B-поле

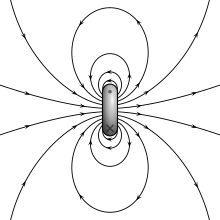
Магнітне поле B, створене контуром зі струмом

У цій моделі диполь розглядається як маленький замкнений контур, по якому беззупинно тече струм^[8]. В такій моделі, поле що він створює буде соленоїдним, тобто його силові лінії не будуть мати ні початку, ні кінця, а будуть закручені навколо контуру, проходячи через його серцевину. Магнітний момент такого диполю буде рівним m = IS, де I — сила струму в контурі, а S — площа його перерізу. Вісь такого магніту буде перпендикулярною контуру. Важливою відмінністю B-поля є те, що на відміну від H-поля, лінії якого завжди напрямлені від одного полюсу до іншого, його лінії всередині магніту мають зворотній напрямок.

Узагальнюючи і формалізуючи, можна сказати, що якщо силова лінія В-поля входить у деяку область простору, то вона завжди пізніше виходить з неї, тобто

∮S⁡B⋅dA=0,displaystyle oint _Smathbf B cdot mathrm d mathbf A =0,

де інтеграл береться по деякій замкненій поверхні S, а добуток B · dA — позитивний, якщо лінія входить всередину поверхні, і негативний, якщо вона виходить з неї.

Фактично, токова модель є ближчою до істини, ніж полюсна — для багатьох частинок, наприклад, для перехідних металів або двохатомних молекул, основний вклад в магнітний момент дає орбітальний момент електрона.^[9] Проте інше джерело — момент, що з'являється завдяки спінам електронів і ядер, не пояснюється такою моделлю, бо спін є суто квантовим явищем, і не має близьких аналогів в макросвіті.

Електричні заряди

Правило правої руки: струм, що рухається в напрямку, заданому білою стрілкою, створює магнітне поле, що позначене червоними стрілками

Поодинокий заряд що рухається рівномірно і прямолінійно, створює навколо себе магнітне поле, лінії якого є замкненими, і закрученими навколо вісі, що збігається з напрямком руху заряду. Його величину можна записати як B = E×v.^[10] Як можна зрозуміти з релятивістських міркувань, величина поля буде залежати від системи відліку — для спостерігача, що рухається з тією ж швидкістю і в тому ж напрямку, що і заряд, В = 0. Таким чином, що в теорії відносності електричне і магнітне поле є складовими частинами одного електромагнітного поля.

Оскільки електричний струм є сукупністю великої кількості рухомих зарядів, він також створює магнітне поле. При цьому електричного поля така система може і не створювати, бо є електрично нейтральною. Величина цього поля визначається законом Біо-Савара-Лапласа:

B=μ0I4π∫wiredℓ×r^r2,displaystyle mathbf B =frac mu _0I4pi int _mathrm wire frac mathrm d boldsymbol ell times mathbf hat r r^2,

Напрям поля можна визначити за допомогою правила Ампера або правила правої руки. Таке поле також є вихровим, тобто його силові лінії замкнуті. У крайньому випадку нескінченного прямого провідника магнітне поле буде мати осьову і трансляційну симетрії.

соленоїд

Для концентрації магнітного поля, контур завивають у котушку, утворюючи, таким чином, соленоїд. У соленоїді внутрішнє поле підсилюється, а зовнішнє — послаблюється. У випадку, якщо всередину соленоїда помістити феромагнітне осердя, утворюється електромагніт. Для нескінченного соленоїда, поле всередині нього можна виразити формулою^[11]

B=μ0nIdisplaystyle B=mu _0nI

де n — кількість витків проводу на одиницю довжини, I — сила струму в контурі. Ця формула є вірною і для скінченного соленоїда у випадку, якщо точка вимірювання знаходиться достатньо далеко від його кінців.

Магнітне поле створюється також змінним електричним полем. За законом електромагнітної індукції змінне магнітне поле породжує змінне електричне поле, що також є вихровим. Взаємне створення електричного і магнітного поля змінними магнітним і електричним полем призводить до можливості розповсюдження в просторі електромагнітних хвиль.

Дія магнітного поля

На магніти

Два магніти діють один на одного, проте оскільки ця взаємодія є диполь-дипольною, то її закон є доволі складним і залежить від орієнтації магнітів. Втім, якщо магніти розташовані достатньо далеко один від одного, а їх осі напрямлені в одну сторону, то силу, з якою один діє на інший можна описати як

F=3μm1m22πr4displaystyle F=frac 3mu m_1m_22pi r^4

де m₁ і m₂ — магнітні моменти.
З рівняння видно, що сила взаємодії між магнітами падає досить швидко — пропорційно четвертому ступеню відстані між ними.^[12]

Магніти взаємодіють і зі звичайними речовинами. За характером цієї взаємодії, всі речовини поділяються на^[13]:

• 
  Діамагнетики — завжди намагнічуються проти магнітного поля, тобто мають від'ємну магнітну сприйнятливість і відштовхуються будь-яким полюсом магніту. Не мають магнітних властивостей за відсутності зовнішнього поля.


• 
  Парамагнетики — слабко намагнічуються вздовж зовнішнього магнітного поля, тобто мають додатну магнітну сприйнятливість. Магнітна проникність близька до одиниці. Не мають магнітних властивостей за відсутності зовнішнього поля.


• 
  Феромагнетики — для таких речовин характерний далекий порядок магнітних моментів атомів. Через це, такі речовини можуть мати власний вектор намагніченості навіть за відсутності зовнішнього магнітного поля, хоча ця намагніченість і змінюється під дією зовнішнього поля. Магнітна сприйнятливість феромагнентиків додатня і значно більша за одиницю.


• 
  Антиферомагнетики — як і для попередньої групи, магнітні моменти атомів таких речовин мають дальній порядок, проте на відміну від феромагнетиків, моменти сусідніх атомів направлені антипаралельно, і тому компенсують один одного, а загальна намагніченість речовини лишається близькою до нуля.


• 
  Ферімагнетики — як і в антиферомагнетиках, ці речовини мають антипаралельно напрямлені магнітні моменти атомів, але при цьому атоми, що направлені в одну сторону мають більший момент, ніж ті, що направлені в іншу, а тому вони не компенсують один одного, і речовина має ненульову намагніченість.

На електричні заряди

Дія магнітного поля на рухомі заряди визначається силою Лоренца, що (у системі СІ) дорівнює:

F=q[v×B]displaystyle mathbf F =q[mathbf v times mathbf B ].

Тобто, ця сила напрямлена перпендикулярно швидкості заряду і напрямку магнітного поля. Через це робота, що її виконує магнітне поле над частинкою, дорівнює нулю. У разі відсутності інших сил, частинка в магнітному полі рухається по колу. У випадку наявності іншого поля, що діє на неї, наприклад, електричного, траєкторія перетворюється на гвинтову лінію.

Оскільки електричний струм є просто великою кількістю рухомих зарядів, на провідник в магнітному полі також діє сила. Ця сила називається силою Ампера. Вона дорівнює

F=BILsin⁡αdisplaystyle F=BILsin alpha !

Де L — довжина відрізка провідника.
Оскільки, за законом Біо-Савара-Лапласа, провідник зі струмом сам створює навколо себе магнітне поле, з цього витікає, що на два провідники, по яким тече струм, також діє сила Ампера — якщо струми течуть в одному напрямку, то провідники притягуються, а якщо в протилежних — відштовхуються.

Енергія магнітного поля

Енергія магнітного поля в просторі задається формулою

W=18π∫B⋅HdVdisplaystyle W=frac 18pi int mathbf B cdot mathbf H dV.

Відповідно, густина енергії магнітного поля дорівнює

w=18πB⋅Hdisplaystyle w=frac 18pi mathbf B cdot mathbf H .

Енергія магнітного поля провідника зі струмом дорівнює:

W=12LI2displaystyle W=frac 12LI^2,

де Idisplaystyle I — сила струму, а Ldisplaystyle L — індуктивність, що залежить від форми провідника.

Термодинаміка

В зовнішньому магнітному полі, яке задається вектором магнітної індукції Bdisplaystyle mathbf B змінюються значення термодинамічних потенціалів термодинамічних систем. Так, наприклад, приріст внутрішньої енергії одиничного об'єму термодинамічної системи при зміні величини індукції магнітного поля на dBdisplaystyle dmathbf B дорівнює

dU=TdS+14πH⋅dBdisplaystyle dU=TdS+frac 14pi mathbf H cdot dmathbf B ,

де S — ентропія, T — температура.

Відповідно, для вільної енергії

dF=−SdT+14πH⋅dBdisplaystyle dF=-SdT+frac 14pi mathbf H cdot dmathbf B

Таким чином, напруженість магнітного поля в термодинамічній системі визначається через часткову похідну від вільної енергії при сталій температурі

H=4π(∂F∂B)Tdisplaystyle H=4pi left(frac partial Fpartial Bright)_T

Електромагнетизм у релятивістській фізиці і квантовій теорії поля

В теорії відносності електричне і магнітне поле розглядаються як прояви єдиного електромагнітного поля. Воно описується 4-тензором електромагнітного поля а також 4-потенціалом електромагнітного поля. Розгляд електромагнітного поля як єдиної сутності дозволяє значно спростити рівняння Максвелла, формулювання електродинаміки через лагранжіани, та інші. Також у такому випадку стає легше розширити рівняння для електромагнітного поля з урахуванням гравітаційного поля.

Електромагнітне поле квантується — його частинкою-носієм є фотон.

Лагранжіан поля в квантовій електродинаміці записується як дійсна частина наступного рівняння^[14][15]:

L=ψ¯(iγμDμ−m)ψ−14FμνFμνdisplaystyle mathcal L=bar psi (igamma ^mu D_mu -m)psi -frac 14F_mu nu F^mu nu

де

γμdisplaystyle gamma ^mu  — матриці Дірака;

ψdisplaystyle psi  — біспінор електрон-позитронного поля (спінор Дірака);

ψ¯≡ψ†γ0displaystyle bar psi equiv psi ^dagger gamma ^0 — спряження Дірака;

Dμ≡∂μ+ieAμ+ieBμdisplaystyle D_mu equiv partial _mu +ieA_mu +ieB_mu ,! — калібрувально-коваріантна похідна;

e — стала тонкої структури;

m — маса електрона;

Aμdisplaystyle A_mu Лоренц-коваріантний 4-потенціал власного електромагнітного поля електрона;

Bμdisplaystyle B_mu зовнішнє поле довільної природи;

Fμν=∂μAν−∂νAμdisplaystyle F_mu nu =partial _mu A_nu -partial _nu A_mu ,! тензор електромагнітного поля.

Вимірювання

Магнітне поле вимірюється магнітометрами. Механічні магнітометри визначають величину поля за відхиленням котушки зі струмом. Слабкі магнітні поля вимірюються магнітометрами на основі ефекту Джозефсона — СКВІДами. Магнітне поле можна також вимірювати на основі ефекту ядерного магнітного резонансу, ефекту Хола та іншими методами.

Магнітна індукція B вимірюється в Теслах в системі СІ, і в Гаусах в системі СГС. Напруженість магнітного поля H вимірюється в А/м в системі CI і в Ерстедах в системі СГС.

Створення

Магнітне поле широко використовується в техніці й для наукових цілей. Для його створення використовуються постійні магніти та електромагніти. Однорідне магнітне поле можна отримати за допомогою котушок Гельмгольца. Для створення потужних магнітних полів, необхідних для роботи прискорювачів або для утримання плазми в установках з ядерного синтезу, використовуються електромагніти на надпровідниках.

Див. також

• Магнітне поле Землі


• Магнітний потік


• Квант магнітного потоку


• Магнітний монополь


• Левітація


• Електромагніт


• Густина магнітного потоку

Джерела

Hans Christian Ørsted, Der Geist in der Natur, 1854

• 
  І.М.Кучерук, І.Т.Горбачук, П.П.Луцик (2006). Загальний курс фізики: Навчальний посібник у 3-х т. Т.2. Електрика і магнетизм. Київ: Техніка. 
  

• 
  Сивухин Д.В. (1977). Общий курс физики. т III. Электричество. Москва: Наука. 
  


• Jackson, John David (1999). Classical Electrodynamics (3rd ed.). New York: Wiley. ISBN 0-471-30932-X
  

Примітки